PAST2-H (1-9 Grid)をDPと拡張BFSで通す
これは何か
PAST2をやっていたらHが全く解けず、競プロ鯖で聴いたら強い方がたくさん教えてくれたので2つの解法についてコードとともに解説する記事です!
問題リンク
問題文と制約


自分の考察
解こうとしながらいくつか考えてたことがありました。そのうちいくつかは的外れだったのですが、一応書いておきます。
(少なくとも方針は)合っていた考察
経路に出てくる1~9のループは一順
問題文より、経路に1~9のループが1巡以上含まれていないといけませんが、これが二巡するとしたら1順目の9の次に最短経路でGに行けばよいので、もし二巡目以降が9->Gの最短経路と同じなら無視してもよく、それ以外なら通らない方が経路が短くなります。
グリッド上のBFSを使って解く
グリッド上のある点sからある点tに行くのは、BFSで最短距離が求められます。
ここで罠があって、いつもグリッド上を探索するときは障害物(つまりは通れない点)があるのでBFSが必要ですが、今回の場合は障害物がないので、最短距離は必ずで表せます。これを使うと後述するDPをすることができます。
BFSをしながらDFSをすると解ける
後述しますがこの発想に至る前に一度「S->1」の最短経路を求める、その1の座標を使って「1->2」の最短経路を求める....といった方針でWAしました。サンプルは通っていたのでもっと一般化することで通せると思い、これにたどり着きました。ざっくり言うと「Sから出発して、1を見つけたらそこからいける2を探す」というのを再帰的に続けて、最終的に「8から出発して、9を見つけたらそこからいけるGを探す」「そのGに至るまでの列挙された経路のコストの最小値が答え」という感じです。
結論から言うとこれは合っているのですが、直感に頼って出てきた方針だったので実装が浮かびませんでした...(競プロ鯖の方の力を借りてこれでACすることもできました。)
間違っていた考察
貪欲にBFS
ダメです。反例は
1S213456789G
です(初手で右に行くのが最適だが貪欲BFSでは左に行ってしまう)
ここで諦める
分からなくなった、というか、「BFSしながらDFS」の実装ができなくて諦めました。
解説を開いたら「DPだよ」って書いてありましたが、グラフ問として解きたかったので競プロ鯖で質問してみました。(DP解法についても下の方にまとめてあります)

- なぜ貪欲BFSが通らないのか
- BFSでやるのはひと工夫いる
ということを教わり、square1001氏がまずは JOI - チーズという問題を解くといい、と教えてくれました。
これは今回の各数字が一つしかないバージョンだったので、僕が考えた貪欲BFSでも通りました。これは目標がN個ある場合、N回のBFSが必要になる解法です
ところがsquare1001氏によると
- この問題は一回のBFSでも解ける
- その解法がこのPAST2-Hにつながるヒントになる
ということだったので、考えてみました。有向グラフとして見るとか、始点から各目標への経路のうち交差している部分を引く、とかいろいろ考えたのですが結局わかりませんでした。ギブアップです。ということで以下答え合わせです。
以下解法の話です(ただし、まずはチーズについての解答です)
グラフを拡張する
「グラフを拡張してBFS」というのが答えでした。最初どういう意味かよくわからなかったのですが、しの氏に丁寧に解説を受けてやっと理解できました。
僕のやった貪欲BFSというのはつまり、点sから点tへの最短経路を求めるたびにグラフを使い捨てて新しいものに変えていました。絵で描くと下のようなイメージです
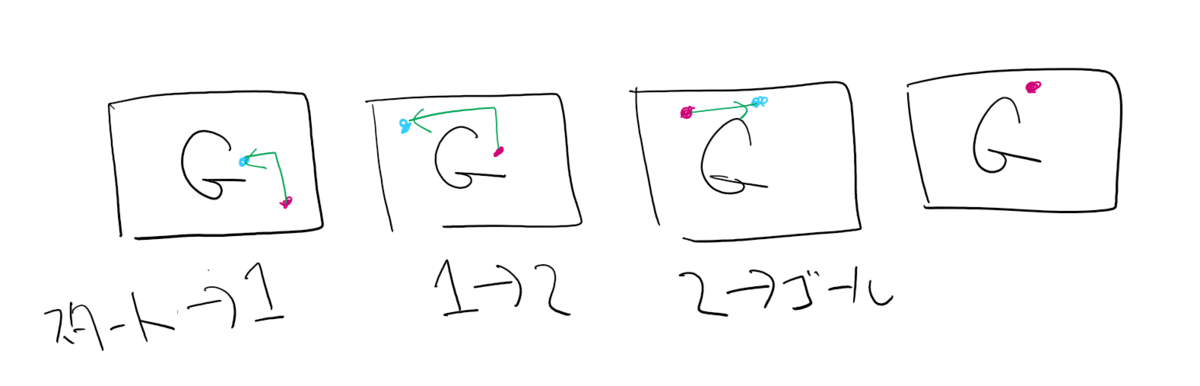
これを、縦に積みます
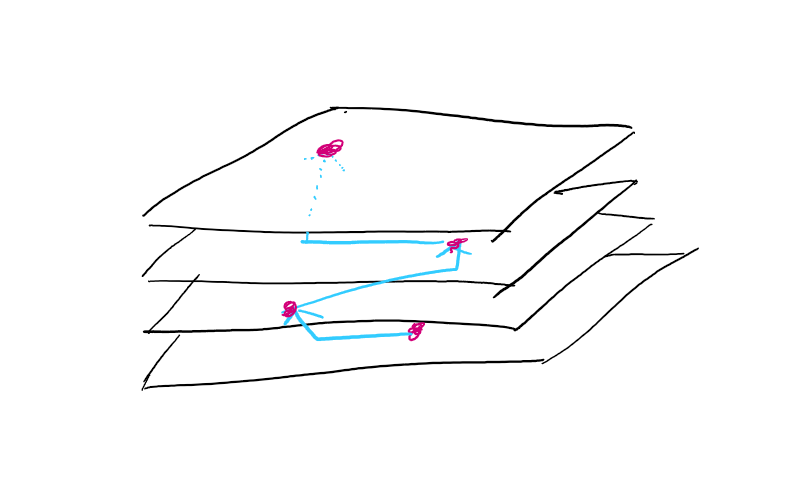
ここで大事なのですが、本質的には横に並べても縦に並べても違いありません。これはイメージの問題であって、本当のバグっていた点は「使い捨てにしていた=一枚のグラフで1ペア分の最短経路しか計算していなかった」です。すなわち、この操作の本質は「N個のグラフ」として扱っていたものを「一つのグラフ」として統合して考えるということです。元のグラフから見ると頂点と辺を拡張しているといえるので、「グラフの拡張」と表現されているようです。
さて、では一つのグラフとしてみることで何ができるようになったかを見ていきます。(まだ話は「チーズ」についてです)
先ほどは(S, 1)や(1, 2)などのペアそれぞれについてグラフを用意してBFSをしていましたが、この操作のおかげで一つのグラフの探索で始点から終点までの最短経路が求められるようになっています。
三次元グリッドの探索なので二次元の時と比べて実装を少しだけ変更する必要があります。具体的には
- 頂点の表現方法
- queueへの頂点の追加
が少しだけ変わります。どういうことか説明していきます。
頂点の表現方法
このグラフでは同じグリッドが何枚も重なっています。それぞれのグリッドの頂点は(x, y)の二次元タプルで表されますが、ここに階層の情報を追加する必要があるので、
を表すと定義します。これが一つ目の(小さな、しかし大事な)変更点です
queueへの頂点の追加
もう一つの変更点は、queueへの頂点の追加の際の条件分岐と追加する情報そのものです。僕は普段二次元グリッドに対するBFSの頂点追加部分を以下のように書いています
nxy = (nx, ny) # (x, y)から行ける点 if nxy in seen: continue elif graph[nx][ny] == ".": dis[nxy] = dis[(x, y)] + 1 if nxy not in seen: todo.append(nxy) seen.add(nxy)
これを以下のように変更します
if (nx, ny, level) in seen: continue elif graph[nx][ny] == "X": continue elif graph[nx][ny] == str(N) and level==N-1: return dis[(x, y, level)] + 1 elif graph[nx][ny] == str(level+1): nxy = (nx, ny, level+1) dis[nxy] = dis[(x, y, level)] + 1 if nxy not in seen: todo.append(nxy) seen.add(nxy) else: nxy = (nx, ny, level) dis[nxy] = dis[(x, y, level)] + 1 if nxy not in seen: todo.append(nxy) seen.add(nxy)
5つの条件分岐と処理をざっくり説明すると、
- その頂点が訪問済み
- 何もしない
- その頂点が障害物(侵入不可能)
- 何もしない
- その頂点の値がゴールの値 かつ 今いる階層がゴールの層-1
- その頂点までの最短距離を返す
- (2に当てはまらない かつ )その頂点の値が今いる層+1
- 今いる頂点(x, y, level)から一層上の点(nx, ny, level+1)に辺を張る
- その頂点が訪問済みで無いなら
- その頂点をqueueに追加する
- その頂点を訪問済みにする
- それ以外
- 今いる頂点(x, y, level)から同じ層の点(nx, ny, level)に辺を張る
- その頂点が訪問済みで無いなら
- その頂点をqueueに追加する
- その頂点を訪問済みにする
といった感じです。
ちなみに僕の実装だと制約的にMLEを起こすのでPythonの場合delをしないと通らないという欠陥があります(3次元リストを使うなどでどうにかしてください)
ここまで前置きです
前置きがめちゃくちゃ長くなってしまいました。では実際にPAST2-Hを通していきましょう
僕が把握している二つの解法でこの問題を解いていきます。まずはここまで用意を進めた拡張グラフに対するBFSからです。
拡張したグラフに対するBFS
BFS部分の実装
def bfs_gird(graph, start, x_lim, y_lim): seen = {start} todo = deque() todo.append(start) dis = {start: 0} one_steps = ((1, 0), (-1, 0), (0, 1), (0, -1)) while todo: x, y, level = todo.popleft() for dx, dy in one_steps: nx, ny = x + dx, y + dy if not ((0 <= nx < x_lim) and (0 <= ny < y_lim)): continue if (nx, ny, level) in seen: continue elif graph[nx][ny] == "G" and level==9: return dis[(x, y, level)] + 1 elif graph[nx][ny] == str(level+1): nxy = (nx, ny, level+1) dis[nxy] = dis[(x, y, level)] + 1 if nxy not in seen: todo.append(nxy) seen.add(nxy) else: nxy = (nx, ny, level) dis[nxy] = dis[(x, y, level)] + 1 if nxy not in seen: todo.append(nxy) seen.add(nxy) return -1
簡単に言うと「S(始点)の座標(x, y, level)とグラフ」を与えて、存在するなら「S->1->2->3->4->->6->7->8->9->G」となる経路のうち最短のものの手数をBFSで探索して返します。存在しない場合(この順でGにたどり着けなかった)場合は-1を返します。
実装を見ればわかると思いますが、同じグリッドが10層(始点がS~9)重なっているのでグラフを表す二次元リスト自体を10倍する必要はありません。
提出とソースコード
N, M = map(int, input().split()) graph = [list(input()) for _ in range(N)] from collections import deque def bfs_gird(graph, start, x_lim, y_lim): seen = {start} todo = deque() todo.append(start) dis = {start: 0} one_steps = ((1, 0), (-1, 0), (0, 1), (0, -1)) while todo: x, y, level = todo.popleft() for dx, dy in one_steps: nx, ny = x + dx, y + dy if not ((0 <= nx < x_lim) and (0 <= ny < y_lim)): continue if (nx, ny, level) in seen: continue elif graph[nx][ny] == "G" and level==9: return dis[(x, y, level)] + 1 elif graph[nx][ny] == str(level+1): nxy = (nx, ny, level+1) dis[nxy] = dis[(x, y, level)] + 1 if nxy not in seen: todo.append(nxy) seen.add(nxy) else: nxy = (nx, ny, level) dis[nxy] = dis[(x, y, level)] + 1 if nxy not in seen: todo.append(nxy) seen.add(nxy) return -1 for i in range(N): for j in range(M): if graph[i][j] == "S": start = (i, j, 0) print(bfs_gird(graph, start, N, M))
関数の返す値は問題文で要求されているものそのものなので、Sの座標を探して関数に渡し(ここでにすることを忘れないようにしましょう)、返り値を出力すればよいです。
計算量(合っていないかもしれませんが一応考えます)
ちゃんとした解析の仕方をしらないので直感的に考えます。
ある層iから層i+1までBFSをするとき、最悪なのは始点と終点が対角にある、例えば(0, 0)から(N, M)に思えます。その時は層iのグリッドすべてを探索することになります。僕はBFSの訪問済み頂点の管理にsetを使っているので、1頂点ごとに挿入にかかって全体で
でしょうか?
なので、10層分探索することを考えても十分余裕そうです。
実際53msで収まっています(Pythonでの話で、PyPyでは97msでした)
DP
実はこれが想定解です。正直検索すればたくさん解説が出てくると思うので後回しにしてしまいました。
公式解説

考察と方針
2点間の距離
かなり前半で示した(そして多分ここまで読むと昔のことなので忘れていると思う)のですが、今回のグリッドは障害物が無いので、ある頂点sから頂点tまでの最短距離はで表されます。これは以下のような関数で求められます
def distance(s, t): return abs(s[0]-t[0]) + abs(s[1]-t[1])
組み合わせの全列挙
素直に考えれば1~9の値を持つ座標をそれぞれまとめて、それらの全ての組み合わせ(1, 2, 3, ..., 8, 9となる組み合わせのことです)に対してコストを計算すれば答えが出ることが分かります。和がSになるN個の数があるとき、それらの総積が最大になるのは(多分)それぞれS/Nとおいたときなので、1~9の各iについてNM/9個あるとすると、計算量は です。これでは到底間に合わないので、これを削っていきます。
各ステップで最適なもののみを選び取る
簡単のために、始点Sには0, 終点Gには10が書いてあるものとします。
0 -> 1
まず初めに、始点の0が書いてあるマスから1が書いてあるマスまでの最短経路を列挙してみます。0のマスの座標が(x_0, y_0)であり、1が書かれたマスがA_1個あるとすると、A_1通りの(座標, Sからの距離)のペアが作れます。0からそれぞれの座標までの最短距離は先ほど示した式で求めることができます。
1 -> 2
次に、1の書いてあるマスから2が書いてあるマスまでの最短経路の組み合わせを考えていきます。1が書いてあるマスはA_1個あり、2が書いてあるマスはA_2個あるとします。1が書いてあるマスから2が書いてあるマスへの最短経路はA_1 * A_2通りあることが分かります。A_1個のiそれぞれについて(2の書いてあるマスの座標, 1の書いてあるマスiからの最短距離)が計算できるからです。
このままでは結局になってしまいます
i -> i+1
ではここで一般化してiが書いてあるマスからi+1が書いてあるマスへの最短経路の数を数えてみましょう。素直に考えると、当然A_1からA_i+1までの総積です。
これを改善するために気づかないといけないのは、「iからi+1への遷移を考えるとき、i-1からiへの遷移がどうであったかは関係がない」ということです。
i-1が書いてあるマスからiが書いてある特定マスへの遷移はA_i-1通りありますが、そのiのマスからi+1の書いてある特定のマスへの遷移の時に使うのは、A_i-1通りある中の最小のコストだけでよい、ということです。なぜなら、どの座標から来ていたとしてもその後の遷移には影響が無いからです。
この性質を使うと、iの書いてあるマスからi+1の書いてあるマスへの遷移について考えるときにA_1からA_iまでの総積通り考えなければいけなかったものが、A_i-1*A_i通りだけ考えればよいことになりました。
説明がすこし複雑になってしまいましたが、この遷移は漸化式に落とし込むことができ、DPをすることができます。
漸化式
のように定義できます。(初期値は十分に大きい値にしましょう)
とするのを忘れないようにしましょう。
提出とソースコード
N, M = map(int, input().split()) graph = [input() for _ in range(N)] def distance(a, b): return abs(a[0]-b[0]) + abs(a[1]-b[1]) points = [[] for _ in range(11)] for i in range(N): for j in range(M): if graph[i][j] == "S": points[0].append((i, j)) elif graph[i][j] == "G": points[10].append((i, j)) else: points[int(graph[i][j])].append((i, j)) inf = float("inf") dp = [[inf for _ in range(M)] for _ in range(N)] start = points[0][0] dp[start[0]][start[1]] = 0 for i in range(1, 11): for point in points[i]: for prev in points[i-1]: dp[point[0]][point[1]] = min(dp[point[0]][point[1]], dp[prev[0]][prev[1]]+distance(point, prev)) goal = points[10][0] print(dp[goal[0]][goal[1]] if dp[goal[0]][goal[1]] != inf else -1)
簡単に解説すると、マスiが書いてある座標をpoints[i]に入れていって、i=1から10まで更新していきます。
最後にDP配列のゴールの座標にアクセスしてinfのままだったら-1, それ以外ならその値を出力します。
計算量解析
最初に述べた通りあるiが書いてあるマスは最悪でなので、毎回それの二乗回ループを回すことになって
になります
さいごに
めちゃくちゃ長くなってすいません